Hur man gör ett T-test i Excel

Ett T-test är ett sätt att avgöra om det finns statistiskt signifikanta skillnader mellan datauppsättningar, med hjälp av studentens t-fördelning. T-testet i Excel är ett tvåprovstest som jämför medelvärdet för två prover. Den här artikeln förklarar vad statistisk signifikans betyder och visar hur man gör ett T-test i Excel. Instruktionerna i den här artikeln gäller Excel 2019, 2016, 2013, 2010, 2007; Excel för Microsoft 365 och Excel Online.

Vad är statistisk betydelse?

Tänk dig att du vill veta vilken av två tärningar som ger en bättre poäng. Du rullar den första formen och får en 2; rullar du den andra formen och får en 6. Berättar detta att den andra formen brukar ge högre poäng? Om du svarade ”Naturligtvis inte” har du redan en viss förståelse för statistisk betydelse. Du förstår att skillnaden berodde på den slumpmässiga förändringen i poängen varje gång en form rullas. Eftersom provet var väldigt litet (bara en rulle) visade det inte något viktigt. Föreställ dig nu att du rullar varje matris 6 gånger:

• Den första formen rullar 3, 6, 6, 4, 3, 3; Medel = 4,17
• Den andra matrisen rullar 5, 6, 2, 5, 2, 4; Medel = 4,00

Bevisar detta nu att den första formen ger högre poäng än den andra? Antagligen inte. Ett litet urval med en relativt liten skillnad mellan medel gör det troligt att skillnaden fortfarande beror på slumpmässiga variationer. När vi ökar antalet tärningar blir det svårt att ge ett sunt förnuft svar på frågan – är skillnaden mellan poängen resultatet av slumpmässig variation eller är det faktiskt mer sannolikt att man ger högre poäng än den andra? Betydelse är sannolikheten att en observerad skillnad mellan prover beror på slumpmässiga variationer. Betydelse kallas ofta alfa-nivå eller helt enkelt ‘α.’ Konfidensnivån, eller helt enkelt ‘c’, är sannolikheten att skillnaden mellan proverna inte beror på slumpmässig variation; med andra ord att det finns en skillnad mellan de underliggande populationerna. Därför: c = 1 – a

Vi kan ställa in ‘α’ på vilken nivå vi vill, för att känna oss säkra på att vi har visat betydelse. Mycket ofta används α = 5% (95% konfidens), men om vi vill vara riktigt säkra på att eventuella skillnader inte orsakas av slumpmässig variation kan vi använda en högre konfidensnivå med α = 1% eller till och med α = 0,1 %. Olika statistiska tester används för att beräkna signifikans i olika situationer. T-test används för att avgöra om medelvärdet för två populationer är olika och F-test används för att avgöra om skillnaderna är olika.

Varför testa för statistisk betydelse?

När vi jämför olika saker måste vi använda betydelsestest för att avgöra om den ena är bättre än den andra. Detta gäller för många fält, till exempel:

• I affärer måste människor jämföra olika produkter och marknadsföringsmetoder.
• I sport måste människor jämföra olika utrustning, tekniker och konkurrenter.
• Inom teknik måste människor jämföra olika mönster och parameterinställningar.

Om du vill testa om något presterar bättre än något annat, inom något område, måste du testa för statistisk signifikans.

Vad är en elevs T-distribution?

En elevs t-fördelning liknar en normal (eller Gaussisk) distribution. Dessa är båda klockformade fördelningar med de flesta resultat nära medelvärdet, men vissa sällsynta händelser är ganska långt från medelvärdet i båda riktningarna, kallade distributionens svansar. Den exakta formen på studentens t-fördelning beror på provets storlek. För prover på mer än 30 är det mycket som den normala fördelningen. När provstorleken minskas blir svansarna större, vilket representerar den ökade osäkerheten som kommer från slutsatser baserat på ett litet urval.

Hur man gör ett T-test i Excel

Innan du kan tillämpa ett T-test för att avgöra om det finns en statistiskt signifikant skillnad mellan medel för två prover, måste du först utföra ett F-test. Detta beror på att olika beräkningar utförs för T-testet beroende på om det finns en signifikant skillnad mellan avvikelserna. Du kommer att behöva Analys Toolpak-tillägg möjligt att utföra denna analys.

Kontroll och laddning av tillägget för analysverktygspaket

Följ dessa steg för att kontrollera och aktivera analysverktygspaketet:

1. Välj FIL flik> välj alternativ.

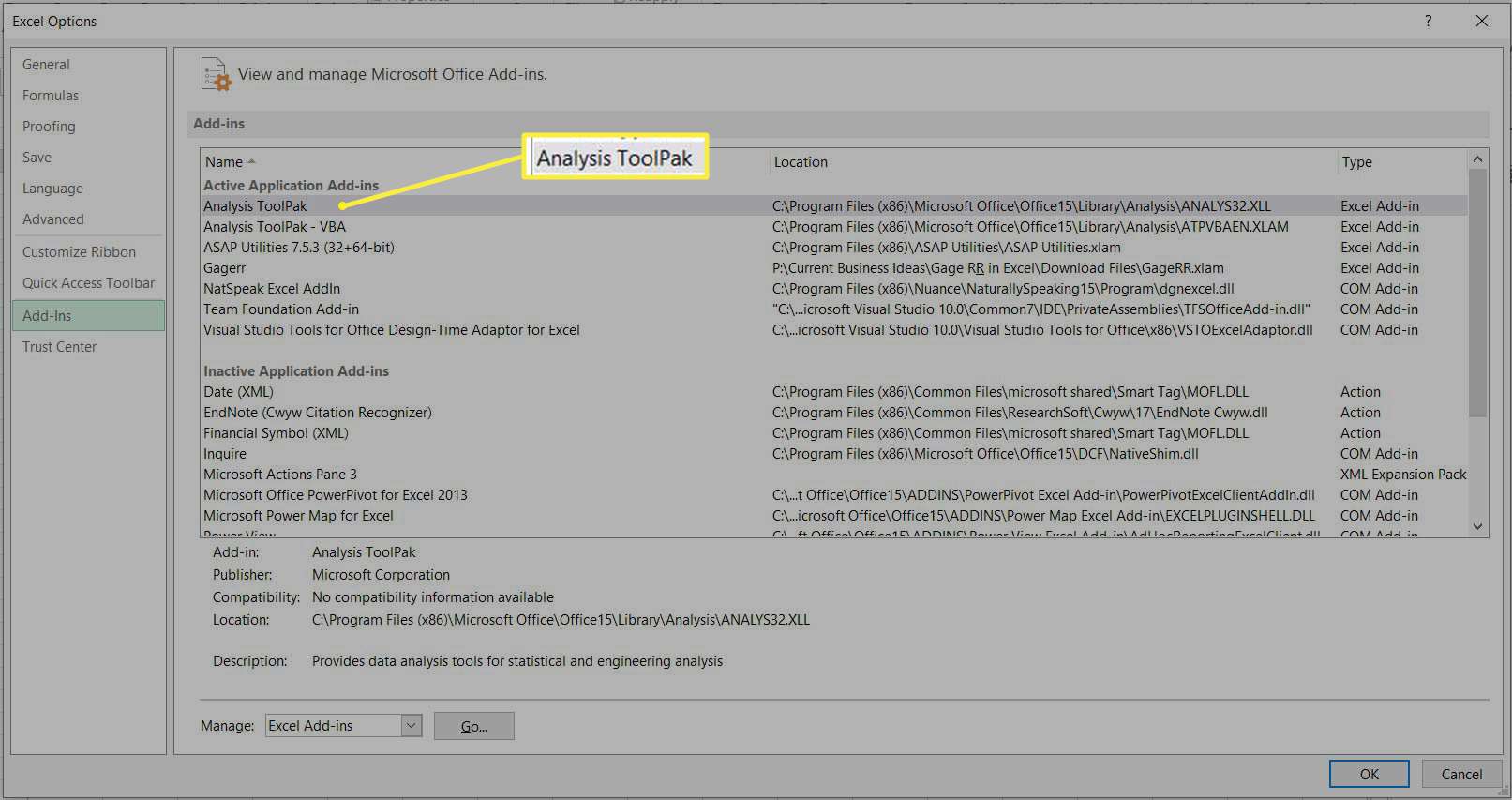
2. I dialogrutan Alternativ väljer du Tillägg från flikarna på vänster sida.

3. Välj Hantera längst ner i fönstret rullgardinsmenyn och välj sedan Excel-tillägg. Välj Gå.

   

4. Se till att kryssrutan bredvid Analysverktygspaket är markerad och välj sedan OK.

5. Analysverktygspaketet är nu aktivt och du är redo att tillämpa F-tester och T-tester.

Utföra ett F-test och ett T-test i Excel

1. Ange två datamängder i ett kalkylark. I det här fallet överväger vi försäljningen av två produkter under en vecka. Det genomsnittliga dagliga försäljningsvärdet för varje produkt beräknas också tillsammans med dess standardavvikelse.

2. Välj Data flik> Dataanalys

3. Välj F-Test tvåprov för avvikelser från listan och välj sedan OK.

   

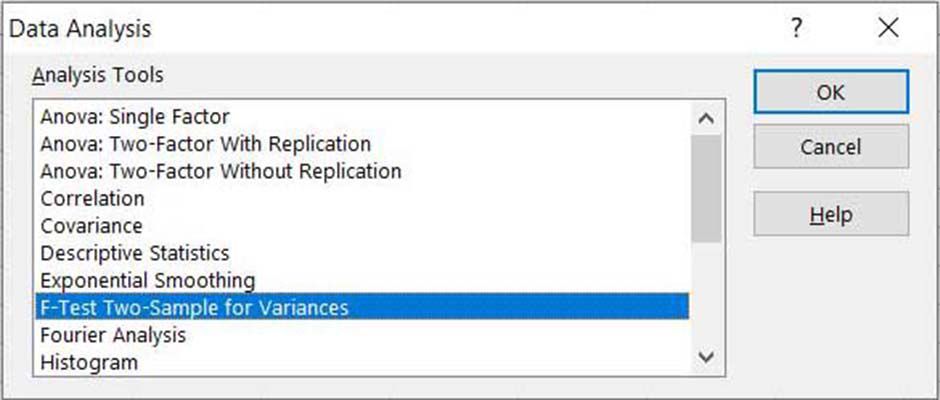
   F-testet är mycket känsligt för icke-normalitet. Det kan därför vara säkrare att använda ett Welch-test, men det är svårare i Excel.

4. Välj Range 1 Variable och Variable 2 Range; ställa in Alpha (0,05 ger 95% konfidens); välj en cell i det övre vänstra hörnet av utdata, med tanke på att detta kommer att fylla 3 kolumner och 10 rader. Välj OK.

   

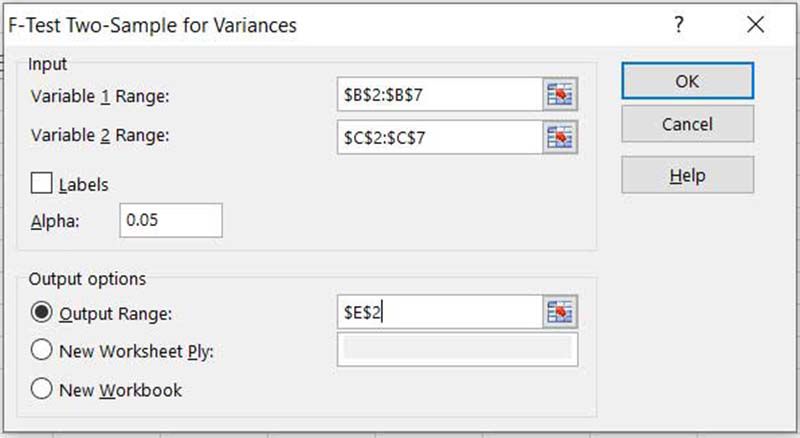
   För området för variabel 1 måste provet med den största standardavvikelsen (eller variansen) väljas.

5. Visa F-testresultaten för att avgöra om det finns en signifikant skillnad mellan avvikelserna. Resultaten ger tre viktiga värden:

   • F: Förhållandet mellan avvikelserna.
   • P (F <= f) en-svans: Sannolikheten att variabel 1 faktiskt inte har en större varians än variabel 2. Om denna är större än alfa, som i allmänhet är 0,05, så finns det ingen signifikant skillnad mellan avvikelserna.
   • F Kritisk en-svans: Värdet på F som krävs för att ge P (F <= f) = α. Om detta värde är större än F, indikerar det också att det inte finns någon signifikant skillnad mellan avvikelserna.

   P (F <= f) kan också beräknas med FDIST-funktionen med F och frihetsgraderna för varje sampel som dess ingångar. Frihetsgrader är helt enkelt antalet observationer i ett prov minus en.

6. Nu när du vet om det finns en skillnad mellan avvikelserna kan du välja lämpligt T-test. Välj Data flik> Dataanalysoch välj sedan antingen t-Test: Tvåprover förutsatt lika avvikelser eller t-Test: Tvåprover förutsatt ojämna avvikelser.

   

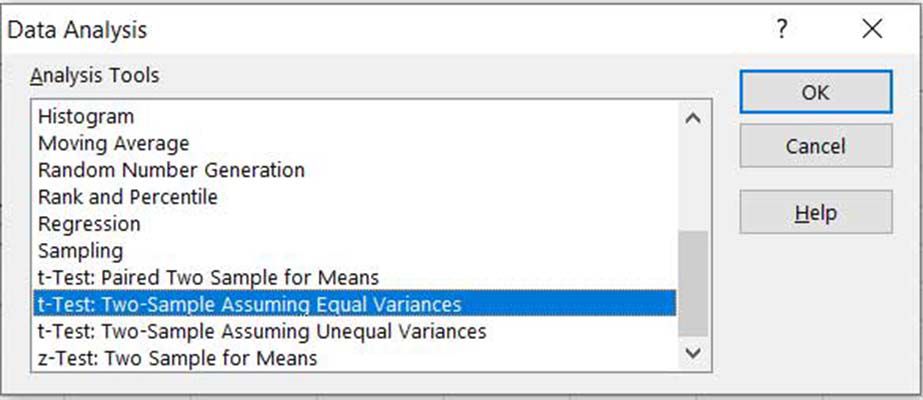
7. Oavsett vilket alternativ du valde i föregående steg kommer du att presenteras med samma dialogruta för att ange detaljerna i analysen. För att börja, välj de intervall som innehåller proverna för Variabel 1 Range och Variabel 2 Range.

   

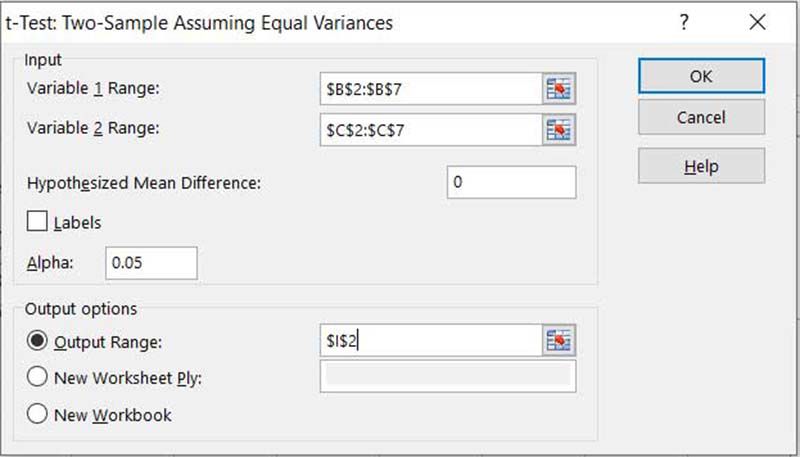
8. Förutsatt att du vill testa för ingen skillnad mellan medel, ställ in Hypoteserad genomsnittlig skillnad till noll.

9. Ställ in signifikansnivån Alpha (0,05 ger 95% konfidens) och välj en cell i det övre vänstra hörnet av utdata, med tanke på att detta kommer att fylla 3 kolumner och 14 rader. Välj OK.

10. Granska resultaten för att avgöra om det finns en signifikant skillnad mellan medel. Precis som med F-testet, om p-värdet, i detta fall P (T <= t), är större än alfa, så finns det ingen signifikant skillnad. I det här fallet finns emellertid två p-värden angivna, ett för ett en-svans-test och det andra för ett två-svans-test. I det här fallet ska du använda tvåstegsvärdet eftersom endera variabeln med ett större medelvärde skulle vara en signifikant skillnad.