Vad är Excel Solver?

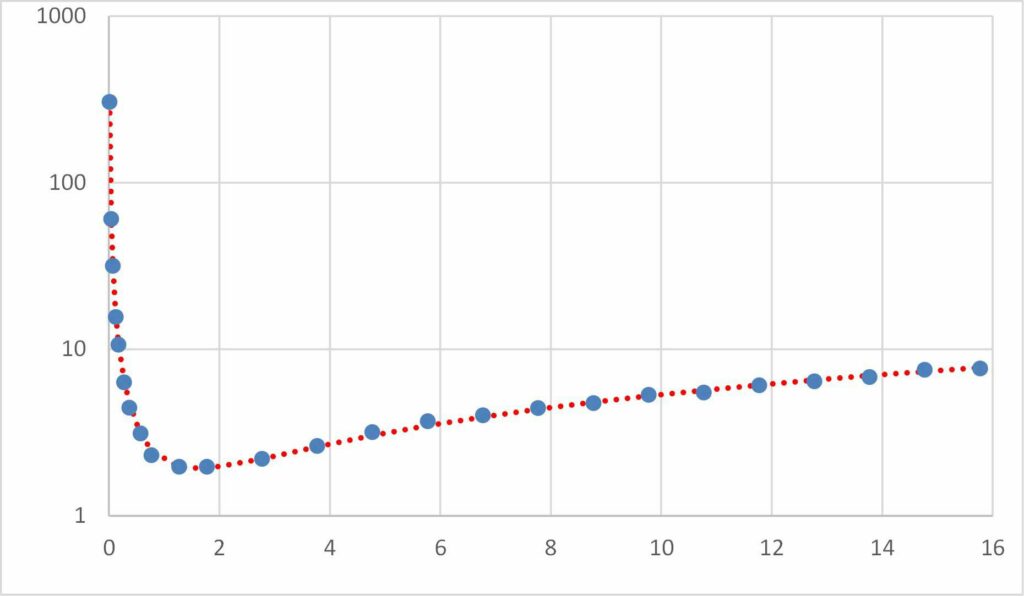
Tillägget Excel Solver utför matematisk optimering. Detta används vanligtvis för att passa komplexa modeller till data eller hitta iterativa lösningar på problem. Du kanske till exempel vill passa en kurva genom vissa datapunkter med hjälp av en ekvation. Lösare kan hitta konstanterna i ekvationen som ger bäst passform till data. En annan applikation är där det är svårt att ordna om en modell för att göra den erforderliga utgången föremål för en ekvation.

Var finns lösare i Excel?

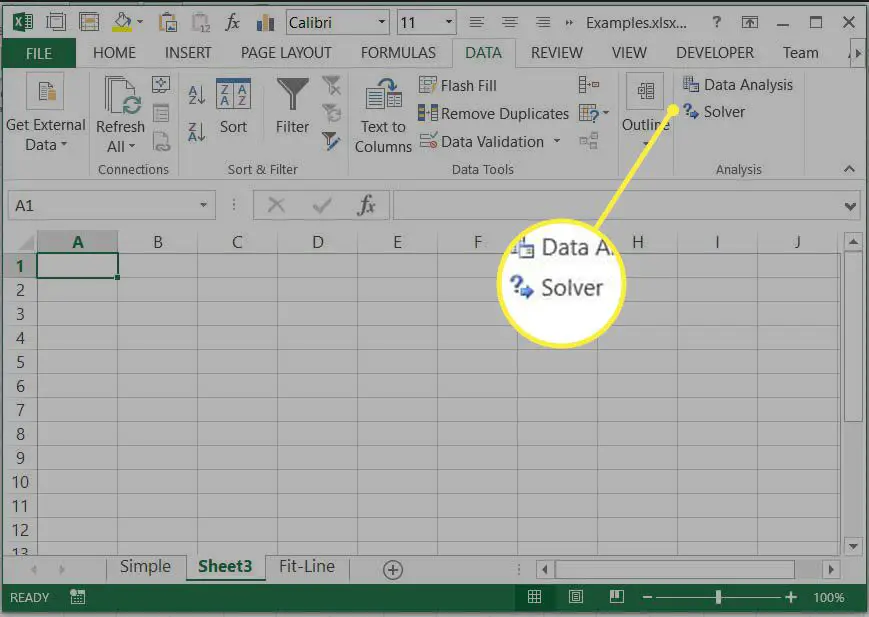
Solver-tillägget ingår i Excel men det laddas inte alltid som en del av en standardinstallation. Välj om du vill kontrollera om den är laddad DATA fliken och leta efter Lösare ikonen i Analys sektion.

Om du inte hittar Solver under DATA-fliken måste du ladda tillägget:

Välj FIL och välj sedan alternativ.
I alternativ dialogruta välj Tillägg från flikarna på vänster sida.
Välj längst ned i fönstret Excel-tillägg från Hantera rullgardinsmeny och välj Gå…
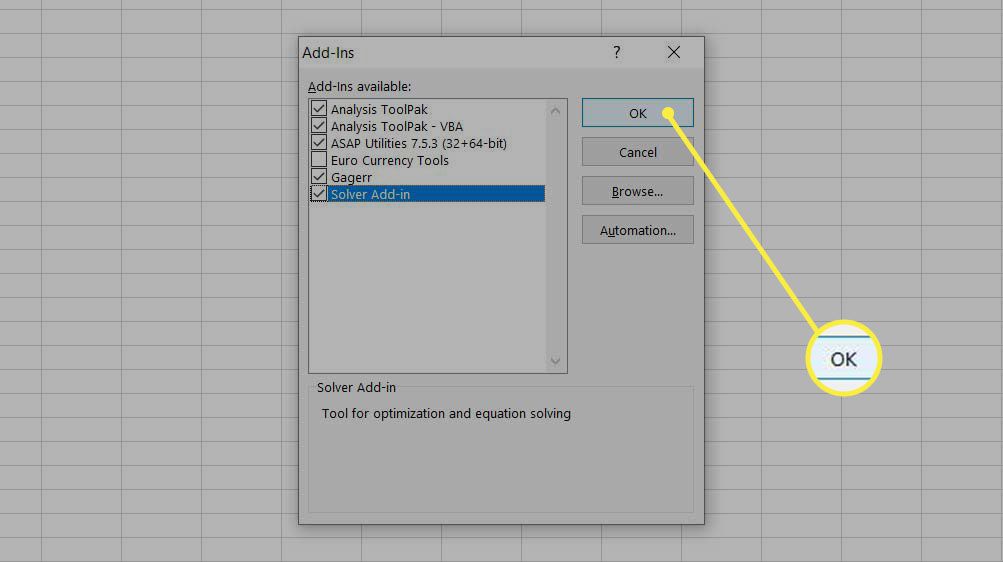
Markera kryssrutan bredvid Solver-tillägg och välj OK.
De Lösare kommandot ska nu visas på DATA flik. Du är redo att använda Solver.

Använda Solver i Excel

Låt oss börja med ett enkelt exempel för att förstå vad Solver gör. Tänk dig att vi vill veta vilken radie som ger en cirkel med ett område på 50 kvadrat enheter. Vi känner till ekvationen för området för en cirkel (A = pi r²). Vi kan naturligtvis ordna om denna ekvation för att ge den radie som krävs för ett visst område, men låt oss till exempel låtsas att vi inte vet hur man gör det. Skapa ett kalkylblad med radien in B1 och beräkna området i B2 med hjälp av ekvationen = pi () * B1 ^ 2.

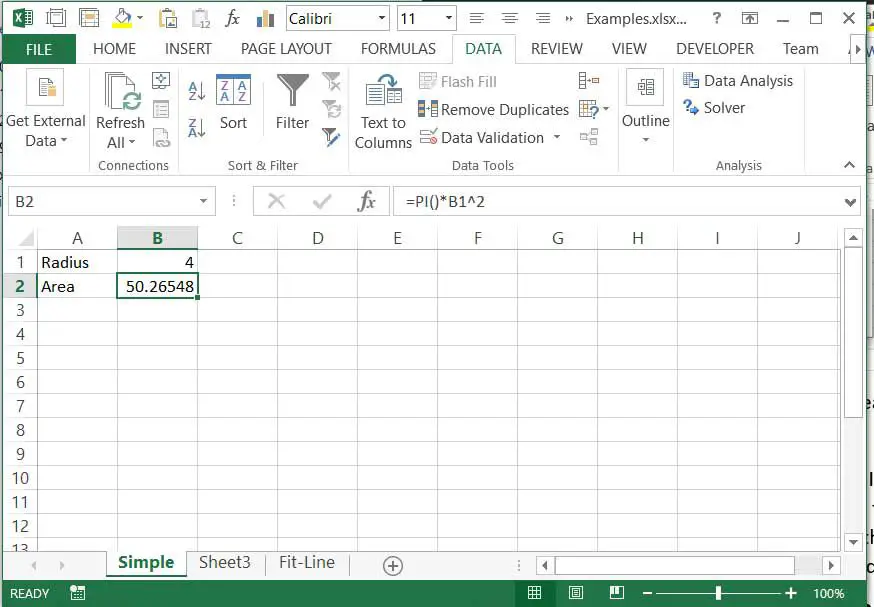
Vi kan justera värdet manuellt B1 fram tills B2 visar ett värde som är tillräckligt nära 50. Beroende på hur exakt vi behöver vara kan detta vara ett praktiskt tillvägagångssätt. Men om vi behöver vara mycket exakta tar det lång tid att göra de justeringar som krävs. Egentligen är det i princip vad Solver gör. Det gör justeringar av värden i vissa celler och kontrollerar värdet i en målcell:

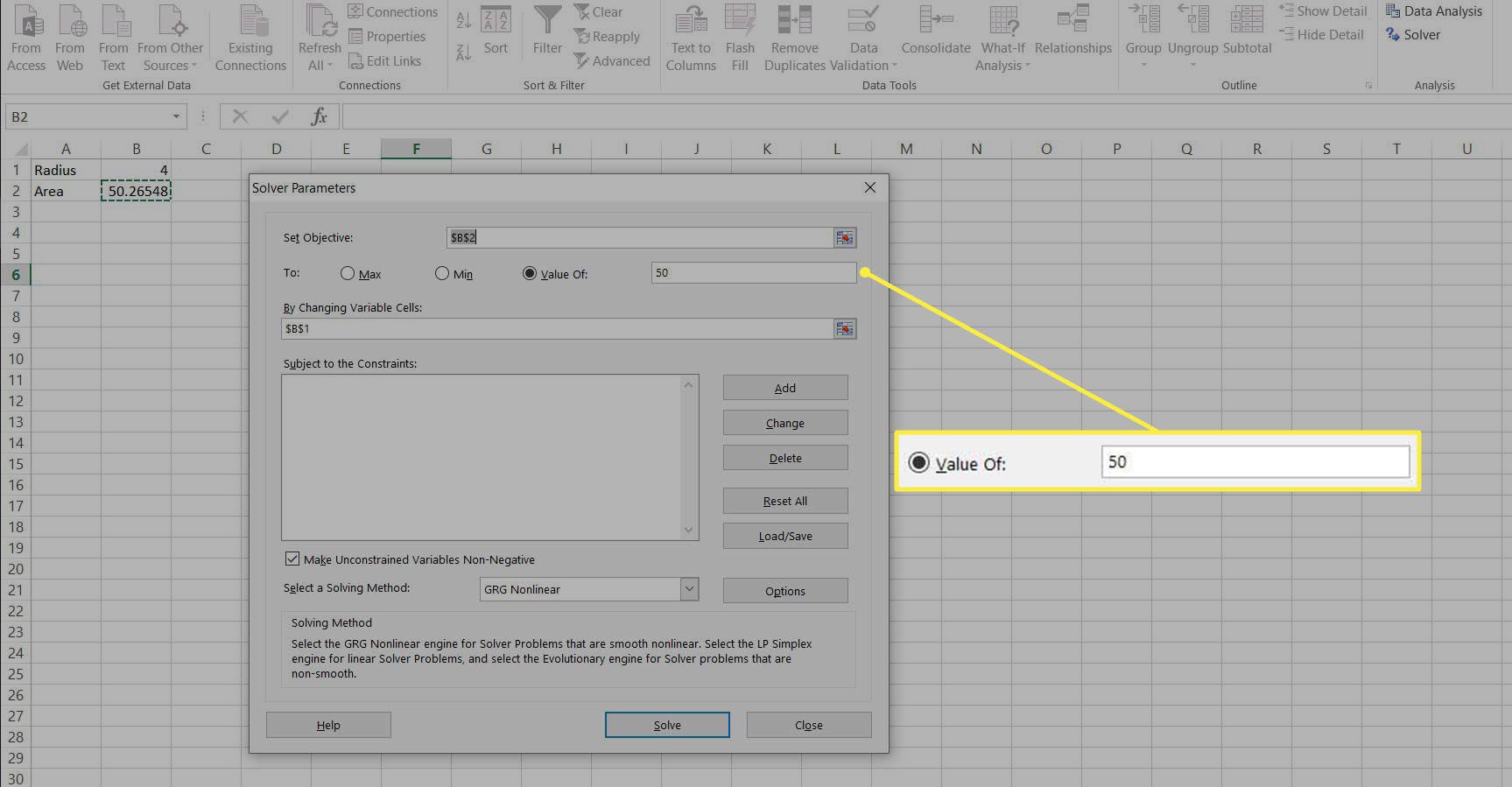
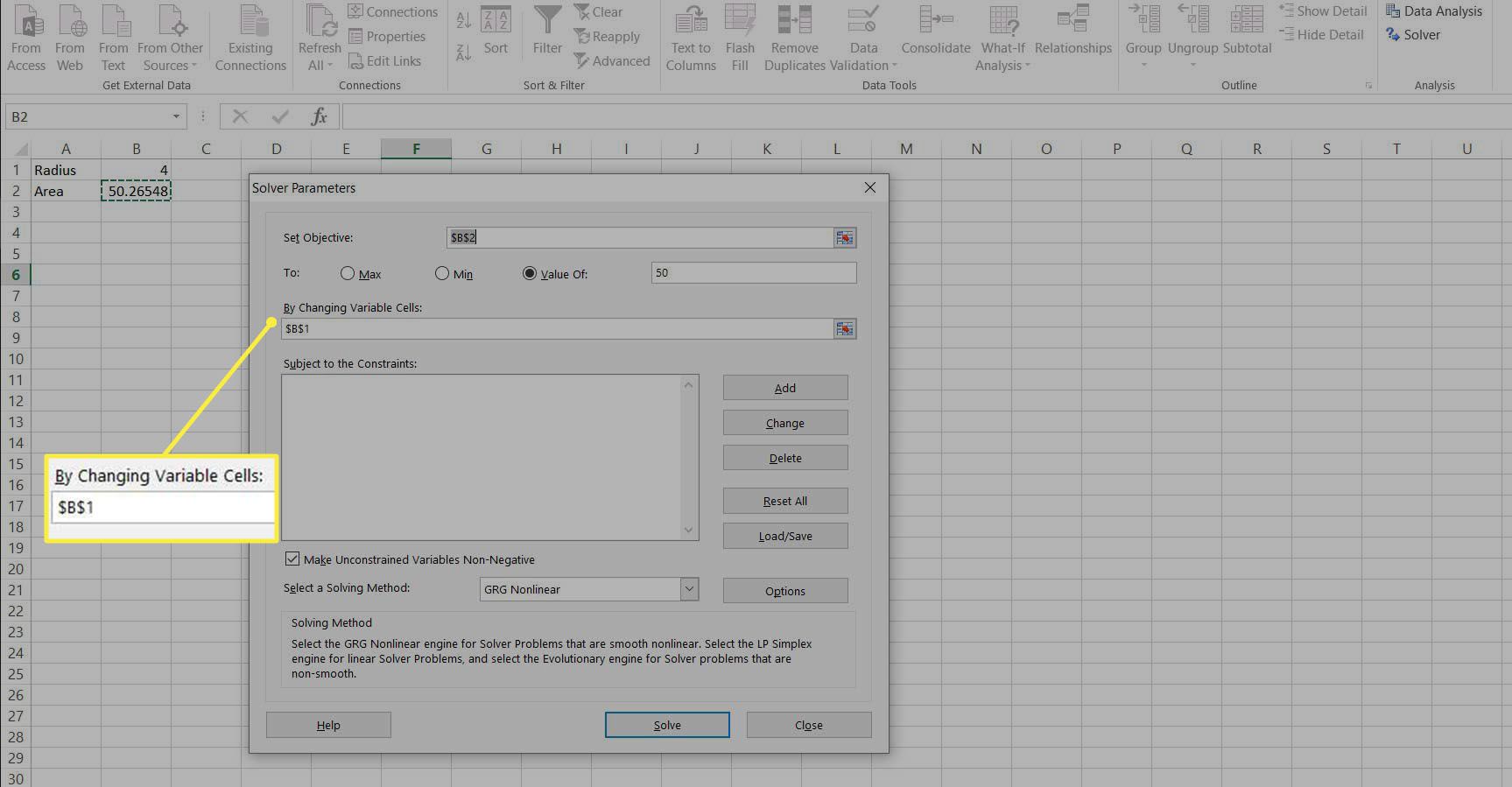
Välj DATA flik och Lösare, för att ladda Lösningsparametrar dialogruta
Ställ in mål cell att vara området, B2. Detta är värdet som kommer att kontrolleras, justera andra celler tills den här når rätt värde.
Välj knappen för Värdet av: och ställ in värdet 50. Detta är det värde som B2 ska uppnå.
I rutan med titeln Genom att ändra variabla celler: ange cellen som innehåller radien, B1.
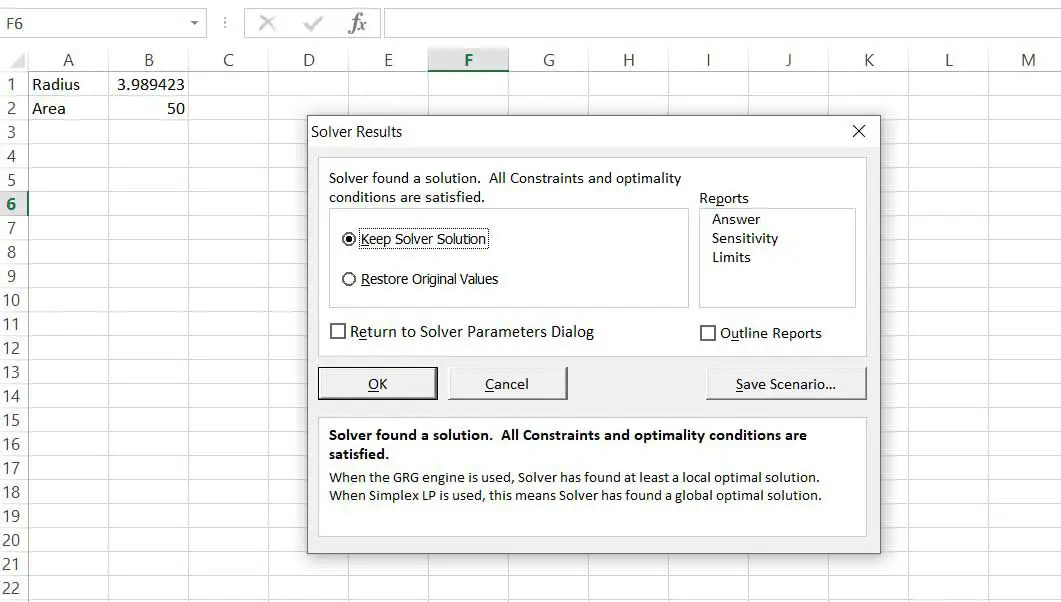
Lämna de andra alternativen som standard och välj Lösa. Optimeringen utförs, värdet på B1 justeras tills B2 är 50 och Lösningsresultat dialogruta visas.
Välj OK för att behålla lösningen.

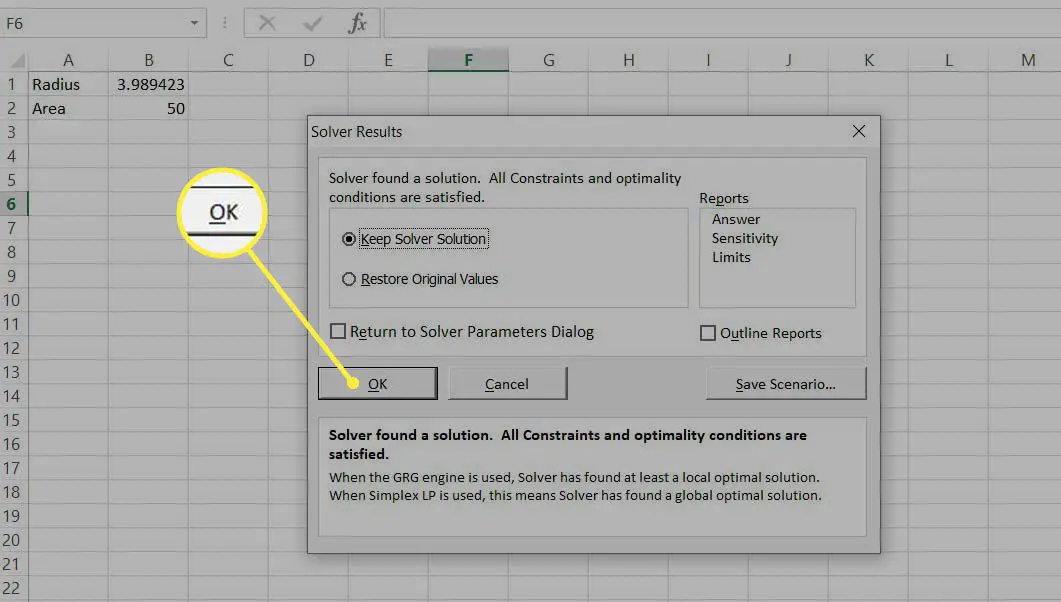
Detta enkla exempel visade hur lösaren fungerar. I det här fallet kunde vi lättare ha fått lösningen på andra sätt. Därefter tittar vi på några exempel där Solver ger lösningar som det skulle vara svårt att hitta på något annat sätt.

Montering av en komplex modell med hjälp av Excel Solver-tillägget

Excel har en inbyggd funktion för att utföra linjär regression, passa en rak linje genom en uppsättning data. Många vanliga icke-linjära funktioner kan lineariseras, vilket innebär att linjär regression kan användas för att passa funktioner som exponentials. För mer komplexa funktioner kan Solver användas för att utföra en minimering av minsta kvadrat. I det här exemplet kommer vi att överväga att anpassa en ekvation av formen ax ^ b + cx ^ d till uppgifterna som visas nedan.

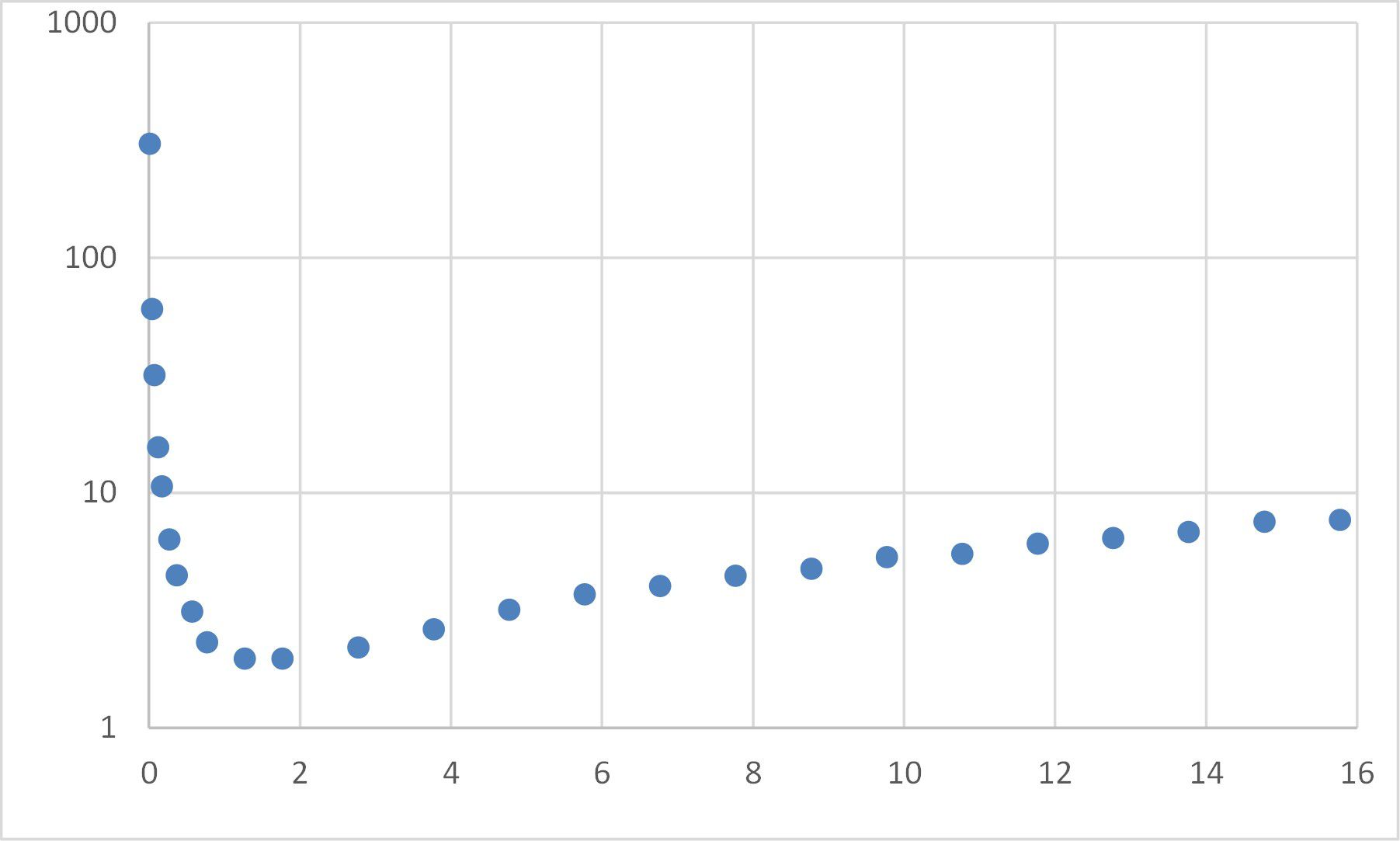
Detta innebär följande steg:

Ordna datauppsättningen med x-värdena i kolumn A och y-värdena i kolumn B.
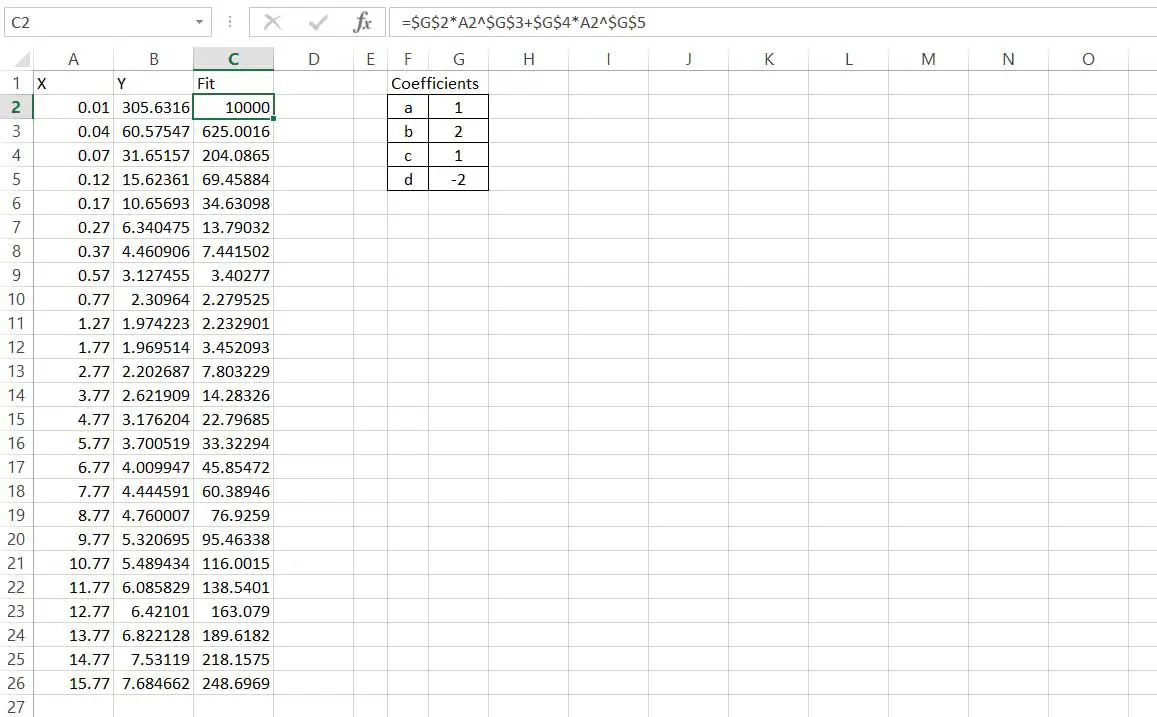
Skapa de 4 koefficientvärdena (a, b, c och d) någonstans i kalkylbladet, dessa kan ges godtyckliga startvärden.
Skapa en kolumn med anpassade Y-värden med en ekvation av form ax ^ b + cx ^ d som refererar till koefficienterna som skapades i steg 2 och x-värdena i kolumn A. Observera att referenser för att kopiera formeln nedåt i kolumnen till koefficienterna måste vara absoluta medan referenserna till x-värden måste vara relativa.
Även om det inte är viktigt, kan du få en visuell indikation på hur bra passform ekvationen är genom att plotta båda y-kolumnerna mot x-värdena på ett enda XY-spridningsdiagram. Det är vettigt att använda markörer för de ursprungliga datapunkterna, eftersom dessa är diskreta värden med brus, och att använda en linje för den monterade ekvationen.

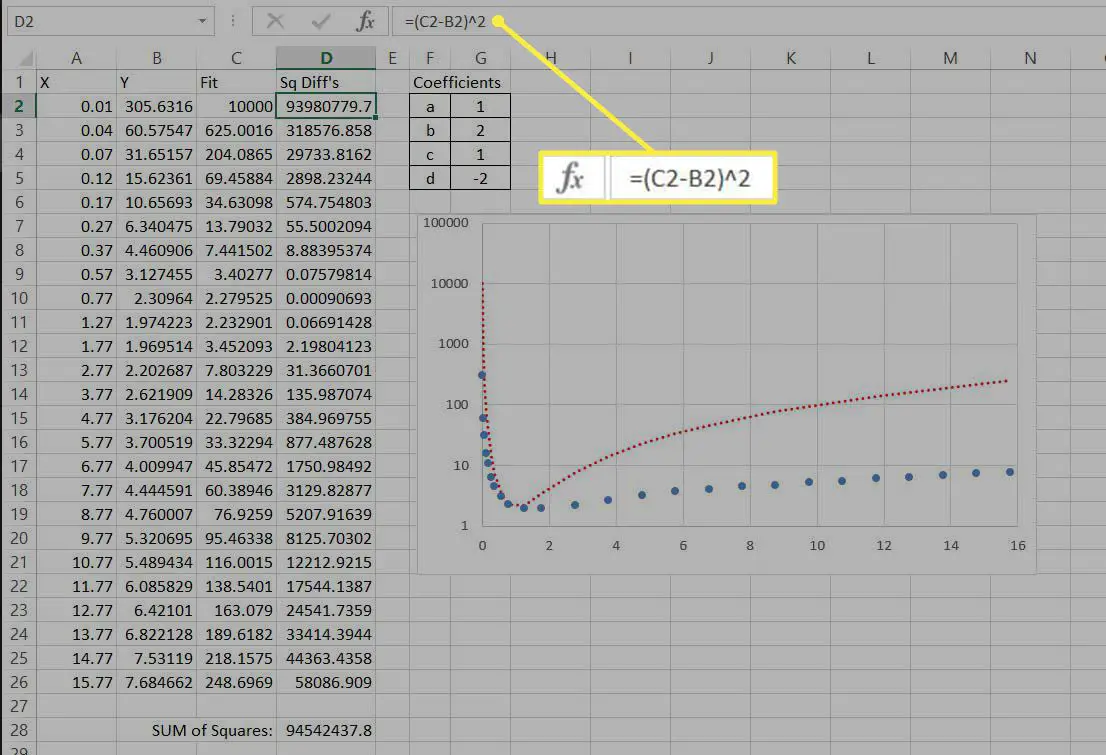
Därefter behöver vi ett sätt att kvantifiera skillnaden mellan data och vår anpassade ekvation. Det vanliga sättet att göra detta är att beräkna summan av kvadratiska skillnader. I en tredje kolumn, för varje rad, subtraheras det ursprungliga datavärdet för Y från det monterade ekvationsvärdet och resultatet kvadreras. Så, in D2, värdet ges av = (C2-B2) ^ 2. Summan av alla dessa kvadratvärden beräknas sedan. Eftersom värdena är kvadrerade kan de bara vara positiva.

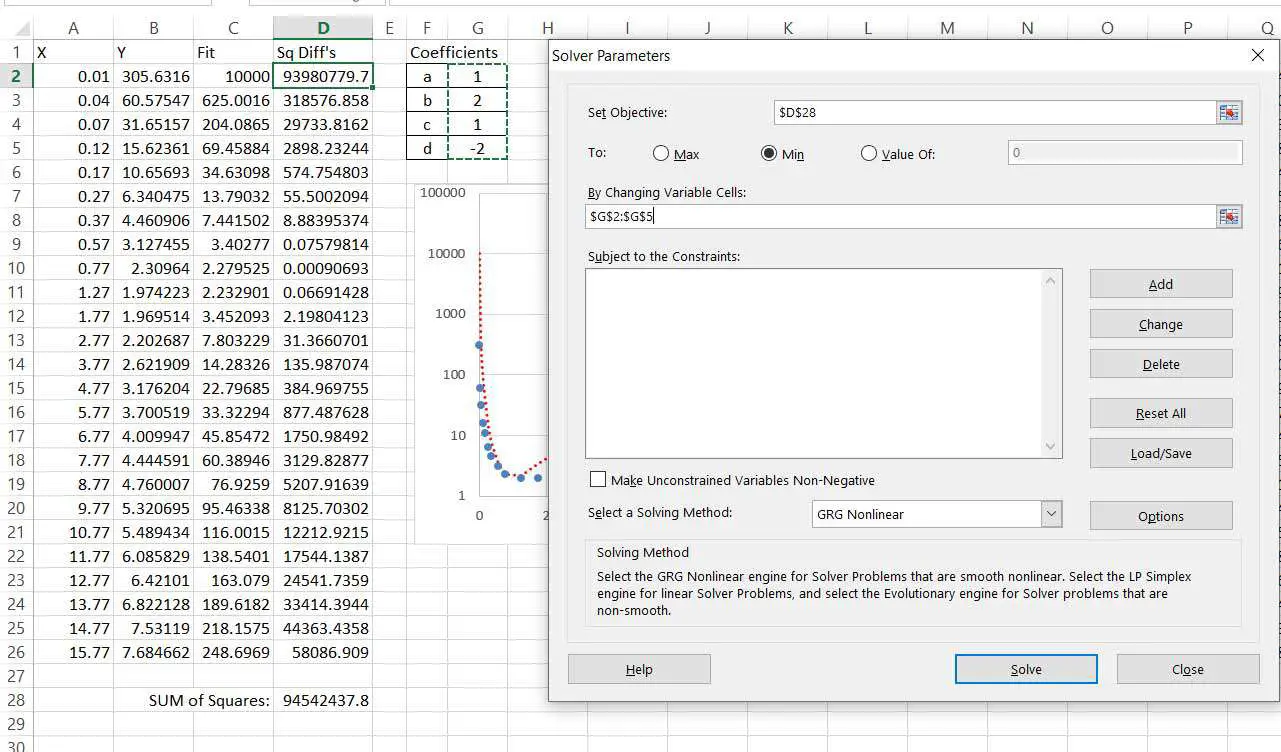
Du är nu redo att utföra optimeringen med hjälp av Solver. Det finns fyra koefficienter som behöver justeras (a, b, c och d). Du har också ett enda objektivvärde att minimera, summan av kvadratiska skillnader. Starta lösaren, som ovan, och ställ in lösarens parametrar för att referera till dessa värden, som visas nedan.

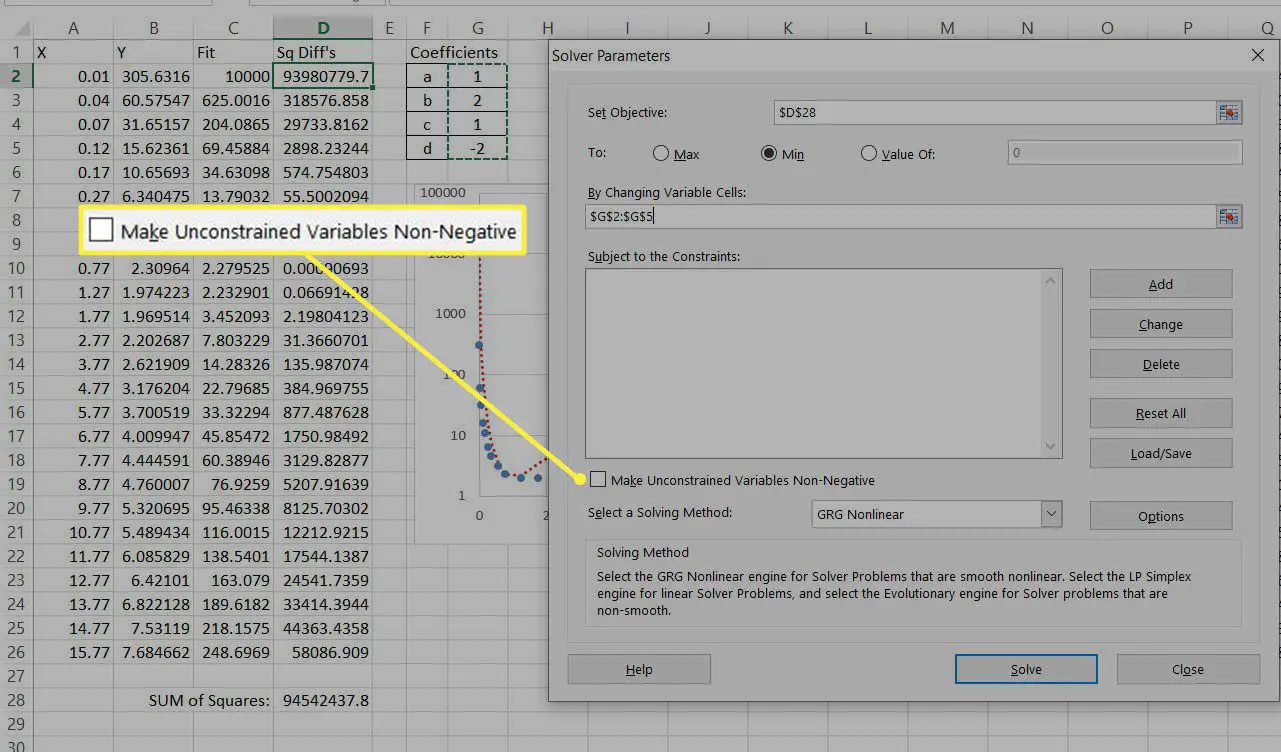
Avmarkera alternativet till Gör obegränsade variabler icke-negativadetta skulle tvinga alla koefficienter att ta positiva värden.

Välj Lösa och granska resultaten. Diagrammet uppdateras och ger en bra indikation på hur bra passformen är. Om lösaren inte får en bra passform vid första försöket kan du försöka köra den igen. Om passformen har förbättrats, försök att lösa från de aktuella värdena. Annars kan du försöka förbättra passformen manuellt innan du löser det.

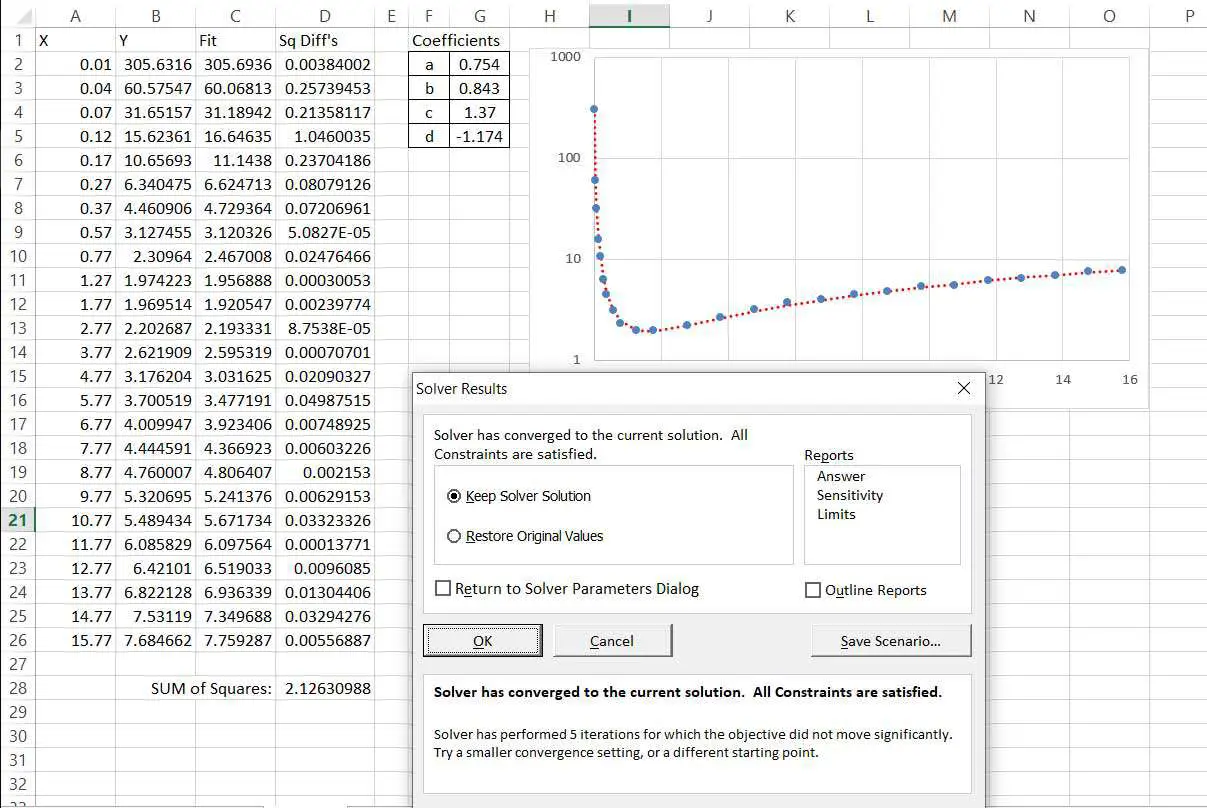
När en bra passform har uppnåtts kan du lämna lösaren.

Lösa en modell iterativt

Ibland finns det en relativt enkel ekvation som ger en output i termer av en del input. Men när vi försöker vända problemet är det inte möjligt att hitta en enkel lösning. Till exempel ges den ström som förbrukas av ett fordon ungefär av P = av + bv ^ 3 där v är hastigheten är a en koefficient för rullmotståndet och b är en koefficient för aerodynamisk dragning. Även om detta är en ganska enkel ekvation, är det inte lätt att ordna om för att ge en ekvation av hastigheten som fordonet når för en given effektingång. Vi kan dock använda Solver för att iterativt hitta denna hastighet. Hitta till exempel den hastighet som uppnåtts med en effektingång på 740 W.

Ställ in ett enkelt kalkylblad med hastigheten, koefficienterna a och b och effekten beräknad från dem.
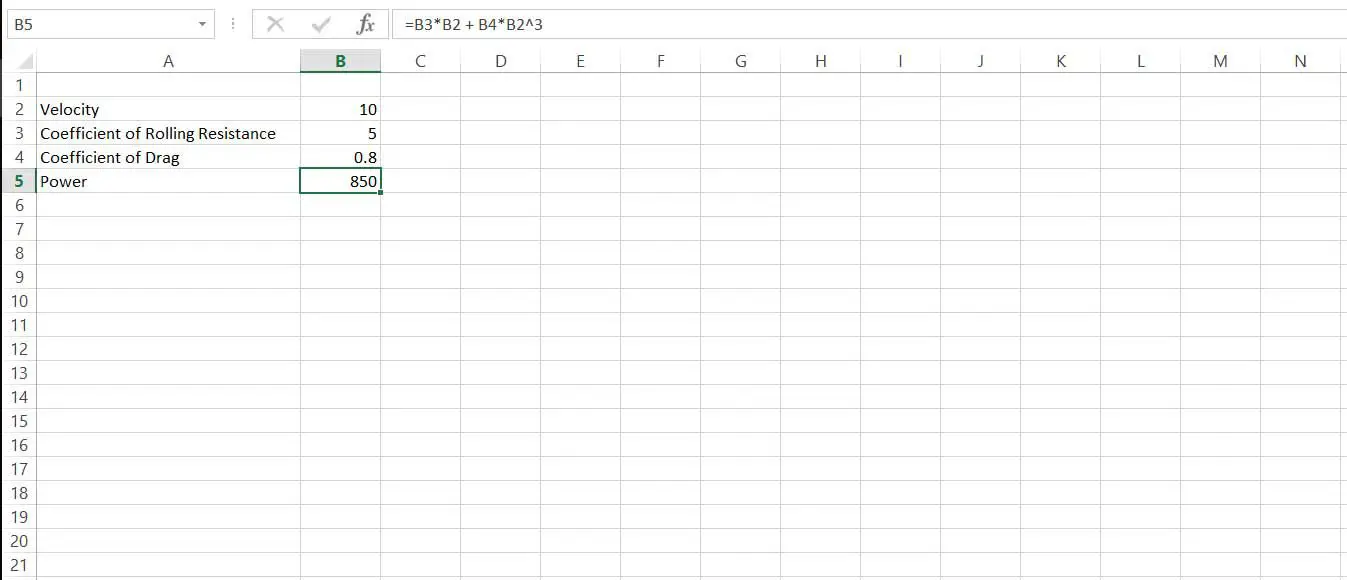
Starta lösaren och ange strömmen, B5, som mål. Ställ in ett objektivvärde på 740 och välj hastigheten, B2, som de variabla celler som ska ändras. Välj lösa för att starta lösningen.
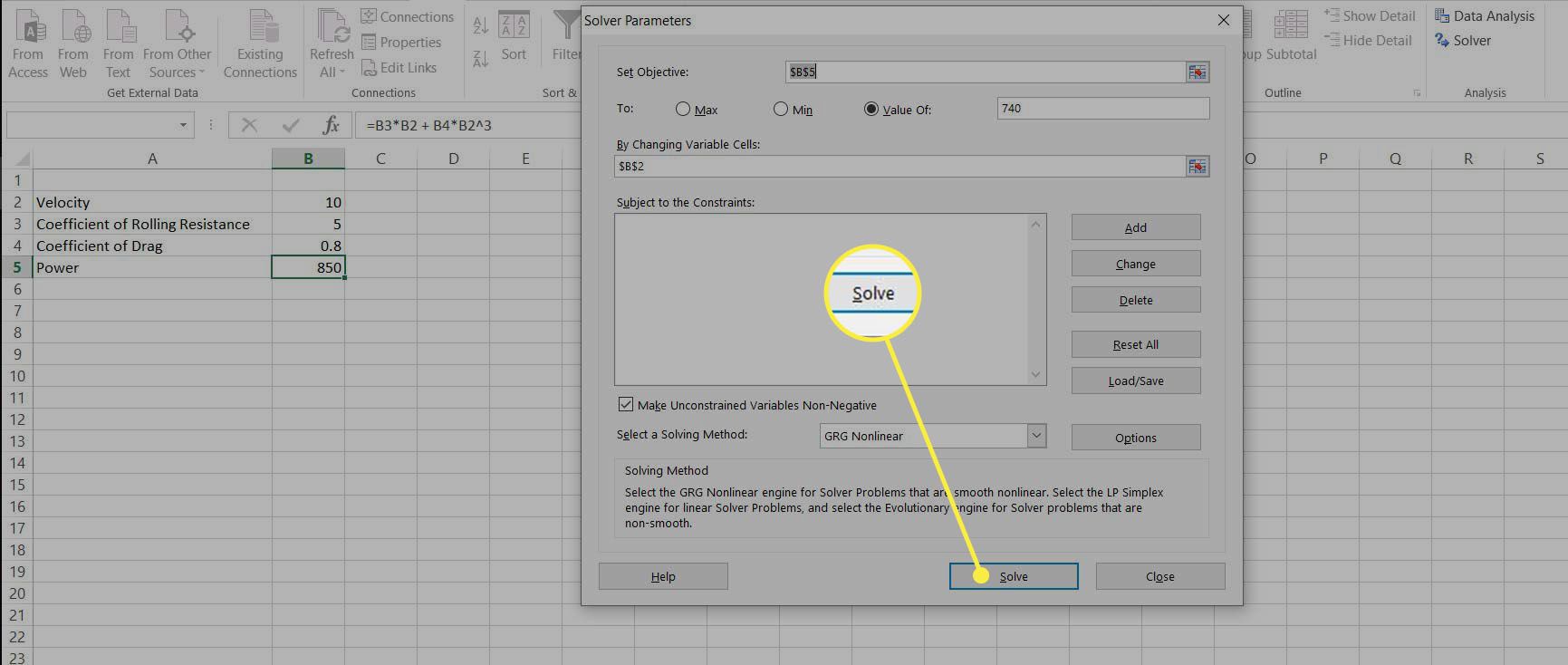
Lösaren justerar hastighetens värde tills effekten är mycket nära 740, vilket ger den hastighet vi behöver.
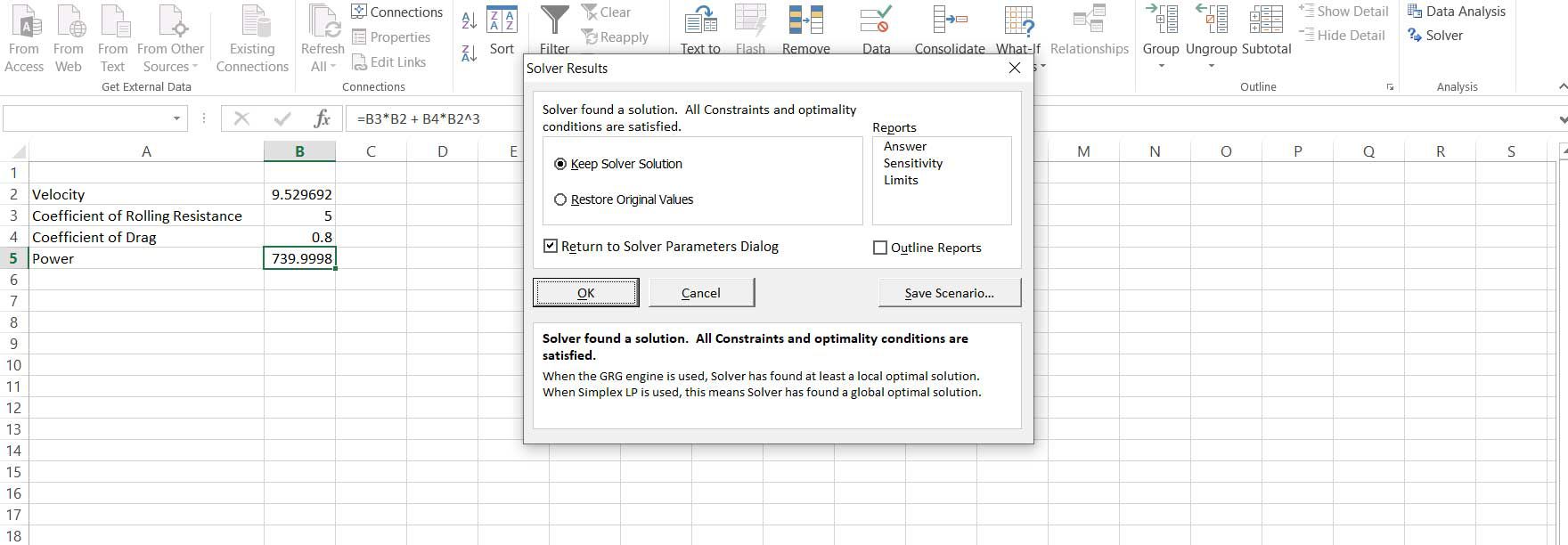
Att lösa modeller på detta sätt kan ofta vara snabbare och mindre felbenägen än att invertera komplexa modeller.

Att förstå de olika alternativen som finns i lösaren kan vara ganska svårt. Om du har svårt att få en förnuftig lösning är det ofta användbart att tillämpa gränsvillkor för de utbytbara cellerna. Dessa är begränsande värden utöver vilka de inte bör justeras. I det föregående exemplet bör till exempel hastigheten inte vara mindre än noll och det skulle också vara möjligt att ställa in en övre gräns. Detta skulle vara en hastighet som du är ganska säker på att fordonet inte kan gå snabbare än. Om du kan ställa in gränser för de föränderliga variabla cellerna, gör det också att andra mer avancerade alternativ fungerar bättre, till exempel multistart. Detta kommer att köra ett antal olika lösningar som börjar vid olika initialvärden för variabler. Att välja lösningsmetod kan också vara svårt. Simplex LP är endast lämplig för linjära modeller, om problemet inte är linjärt kommer det att misslyckas med ett meddelande om att detta villkor inte var uppfyllt. De andra två metoderna är båda lämpliga för icke-linjära metoder. GRG Nonlinear är den snabbaste men lösningen kan vara mycket beroende av de ursprungliga startförhållandena. Det har flexibiliteten att det inte kräver att variabler måste ha gränser. Den evolutionära lösaren är ofta den mest tillförlitliga men det kräver att alla variabler har både övre och nedre gräns, vilket kan vara svårt att träna i förväg. Excel Solver-tillägget är ett mycket kraftfullt verktyg som kan användas på många praktiska problem. För att få full åtkomst till kraften i Excel, försök kombinera Solver med Excel-makron.